Places are containers (light blue disks) which can contain the black balls in the image below. Identify each Place by a token e.g. a.
P = { a, b, c, d, e, f }
Transition (gray boxes) removes the balls from their Places (light blue disks) attached by inbound arrows, and given some arithmetic, move certain counts of them into the Places pointed by transition's outbound arrows.
identify each transition by a token e.g. t1.
T = { t1,t2 }
Example
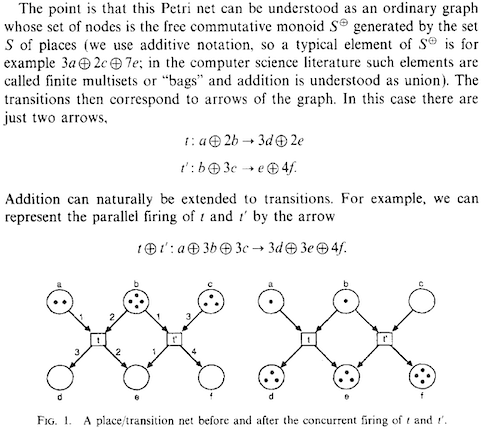
t1: a⊕2b → 3d⊕2e
a⊕2b : a and b disks are attached with inbound arrows to the t1 transition which is rendered as a grey box. Actually a ⊕ 2b is (1 * a)⊕(2 * b) and the two integers are counts of the balls in the corresponding disks.
3d⊕2e : does the arithmetic as follows if there is at least 1 ball in Place 'a' and at least 2 balls in the Place b namely a⊕2b then remove them from the a and b Places and add 3 balls to the outbound Place d and and 2 balls to the outbound Place e namely 3d⊕2e. This act of removing inbound balls and adding outbound balls is called Firing.
Transitions only fire if there are enough inbound balls in all the inbound Places to account for the needed balls for the outbound Places. One or more empty inbound disk(s) do not permit a firing.
'a' in a⊕2b is a Place but 'a' in a⊕b⊕t1⊕t2 is an Id map form 'a' to itself indicating that count of 1 ball in 'a' is indefinitely maintained as in the state of idle or idle transition unless removed by appropriate firings.
Imagine reading a paper like this. No you can code the contents of the most innovative algebras:
¶ monoid[ ]
m = monoid["petri net",{𝐒,𝐓,𝐅,𝐀}];
"petri net" is one of many algebras and in specific monoidal structures for Free Form Programming Language. In order to be universal the function monoid [ ] was designed that based upon the first argument as the name of the monodial structure and the second argument the data for the latter, can construct an instance of the monoid.
As you can see the Free Form programmer can create and define multiple monoids without any limitations.
𝐒 ={ a,b,c,d,e,f};
𝐓 = {t1, t2};
𝐅 = {a → t1, b → t1, b → t2, c → t2, t1 → d, t1 → e, t2 → e, t2 → f};
𝐀 = {
a⊕2*b → 3*d⊕2*e,
b⊕3*c → e⊕4*f
};
m = monoid["petri net",{𝐒,𝐓,𝐅,𝐀}];
x = m[2*a ⊕ 4*b ⊕ 3*c, 6, "my seed"];
y = m[2*a ⊕ 4*b ⊕ 6*c, 10, "my seed"];
xvalue ="x/value";
yvalue ="y/value";
show xvalue also yvalue;
save as petri;
Output
xvalue = a ⊕ b ⊕ 3 * d ⊕ 3 * e ⊕ 4 * f
yvalue = a ⊕ 3 * d ⊕ 4 * e ⊕ 8 * f
¶ m=monoid[...],x=m[...], z="x/.../z"
Free Form programmers can treat the monoidal structures as both a functional form as well as a data form:
- Functional form
x = m[2*a ⊕ 4*b ⊕ 3*c, 6, "my seed"];
- Data in Path Variable form:
arcs = "m/arcs";
show arcs;
Output
arcs = {a -> t1, b -> t1, b -> t2, c -> t2, t1 -> d, t1 -> e, t2 -> e, t2 -> f}
¶ history
𝐒 ={ a,b,c,d,e,f};
𝐓 = {t1, t2};
𝐅 = {a → t1, b → t1, b → t2, c → t2, t1 → d, t1 → e, t2 → e, t2 → f};
𝐀 = {
a⊕2*b → 3*d⊕2*e,
b⊕3*c → e⊕4*f
};
m = monoid["petri net",{𝐒,𝐓,𝐅,𝐀}];
x = m[2*a ⊕ 4*b⊕ 3*c, 6, "my seed"];
history = "x/history";
balls = "x/history/balls";
show history also balls also counts;
Output
history = {
{"(2 a) ⊕ (4 b) ⊕ (3 c)", "updater" -> "(b) ⊕ (3 c)"} -> "(2 a) ⊕ (3 b)"{"(2 a) ⊕ (3 b)", "replacer" -> "(e) ⊕ (4 f)"} -> "(2 a) ⊕ (3 b) ⊕ (e) ⊕ (4 f)"...
, no firing!, no firing!, no firing!, no firing!,
{"(2 a) ⊕ (3 b) ⊕ (e) ⊕ (4 f)", "updater" -> "(a) ⊕ (2 b)"} -> "(a) ⊕ (b) ⊕ (e) ⊕ (4 f)"{"(a) ⊕ (b) ⊕ (e) ⊕ (4 f)", "replacer" -> "(3 d) ⊕ (2 e)"} -> "(a) ⊕ (b) ⊕ (3 d) ⊕ (3 e) ⊕ (4 f)"...
}
balls = {
{"(2 a) ⊕ (4 b) ⊕ (3 c)", "updater" -> "(b) ⊕ (3 c)"} -> "(2 a) ⊕ (3 b)"{"(2 a) ⊕ (3 b)", "replacer" -> "(e) ⊕ (4 f)"} -> "(2 a) ⊕ (3 b) ⊕ (e) ⊕ (4 f)"...
, no firing!, no firing!, no firing!, no firing!,
{"(2 a) ⊕ (3 b) ⊕ (e) ⊕ (4 f)", "updater" -> "(a) ⊕ (2 b)"} -> "(a) ⊕ (b) ⊕ (e) ⊕ (4 f)"{"(a) ⊕ (b) ⊕ (e) ⊕ (4 f)", "replacer" -> "(3 d) ⊕ (2 e)"} -> "(a) ⊕ (b) ⊕ (3 d) ⊕ (3 e) ⊕ (4 f)"...
}
counts = <| a → 1, b → 1, d → 3, e → 3, f → 4 |>
... : separator between the line listings
"updater" : monoidal rule based Term Rewriting
"replacer": simple String-like Rewriting
balls: number of balls in each Place
counts: the very last firing's post transition count of balls in every Place, note that 0 counts are omitted
no firing! : message indicating no transition candidate for firing was available